サバゲーに飽きてしまったので、そのスキマを埋めるべく読書を始めました。
どうせ読むなら読書感想文を公開しようと思います。
記念すべき1冊目はこちら、ル・コルビュジエ著【モデュロールⅠ】です。
この本は、デザインについて勉強をしたい、と思い友人に聞いたところお勧めされたものです。
内容は下記で書くとして、率直な感想として、内容が難しいので各章毎に内容を要約して、小感想を書き、最後にまとめの感想を書きたいと思います。
概要
本のタイトルにもある、モデュロールについての解説と、それにまつわる活動史です。
モデュロールとは、簡単に言うと、統一感のある秩序だった建物のデザインに仕上がる寸法比率のことです。
具体例としては、なんと著者が設計した、国立西洋美術館があります。
画像の右にかかれた数字が、モデュロールの比率を元に求められた値です。
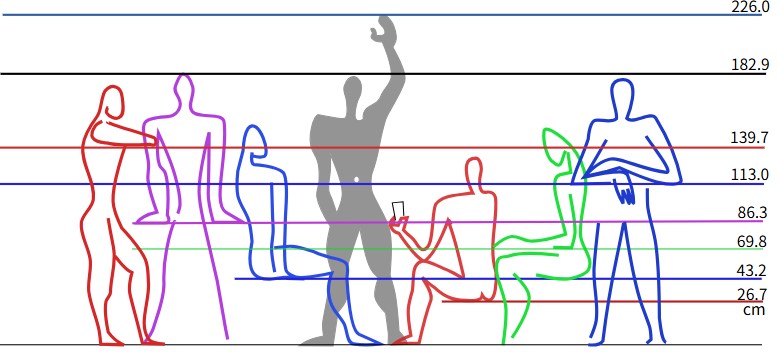
1章 はじめに
要約
まず筆者は、音の12平均律(ドレミファソラシとシャープ、フラット)を例にとり、平均律は音楽を表現する上で必要十分であることをあげました。
一方で、同じ長さを扱う単位にも関わらず、米国のフィート・インチ法とそれ以外の国で採用されているメートル法について、基準となる尺度が大きく異なる点について言及しました。
建築設計では、フィート・インチ法のように人体の長さに基づいた値が適していますが、現代の設計ではメートル法に基づいて作られていいます。
このメートル基準の長さに人体由来の基準の長さを調和されることが設計である、と著者は述べています。
感想
音の平均律が完成されているのは、人の聴力が一定で、物理量である周波数とも整合性が取れているからだと思いました。
一方で、体格は各地域で異なる長さの基準と、世界共通の基準としてメートルが制定された値が建築などの設計でちぐはぐな結果を生むことに納得しました。
また、フィート・インチ法のおかげで起きた事故の例も本文中であげられており、フィート・インチ法のありがたさも再確認できました。
2章 沿革
要約
著者は、黄金比とフィボナッチ数列を組み合わせたModulor(モデュロール:黄金尺)を提案しました。
Modulorは、フランス語のmodule:寸法とsection d’or:黄金比から作られた造語です。
また、”Modulorは、人体寸法と数学から生まれた、寸法をはかる道具である。”と述べています。
本文には、考案した比率を人体にあてはめて、色々な人体の長さや姿勢に当てはまる様子が書かれています。
感想
私は、この2章でこわっと2回もつぶやいてしまいました。
というのも、このModulorは、人体から作られた比率ではなく、無機質な数学の幾何学的図形から導出されたものだったからです。
検索をしても9割が導出された比率しか書いていないのですが、図形から導出された比率が人の長さに当てはまっていくのは吃驚しました。
フィボナッチ数列も高校(?)で習った依頼ですが、まさかこんなところで再会するとは思ってもいませんでした。
3章 数的計算
要約
人のへその高さを基準に
・1倍したものに黄金比を加減したものをフィボナッチ数列で加減算したもの
・2倍したものに黄金比を減算したものをフィボナッチ数列で加減算したもの
を同一のグラフにまとめると、調和の取れた分割比率になることが図を使ってまとめられています。
感想
グラフの点は、フィボナッチ数列に由来するので、点と点の間隔がだんだんと広くなります。
これが”指数”に近いと感じました。
人の間隔というジャンルでは音の大きさも同じかと思い、音の大きさであるデシベルは指数(対数)で表されることと似たものを感じました。
4章 現代における「モデュロールの地位」
省略
5章 最初の応用例
要約
この章では、実際の建築でModulorを使って設計されたものについて紹介していました。
概要
この章で驚いたのは
”マルセイユの工事に使用したすべての寸法の目録をつくらせた。15の寸法ですんだのである。”
私は機械設計が専門ですが、意味なくきれいなメートル基準の寸法にしたり、参考設計があると意味なくその値を真似たりすることがよくあります。
当然、値がはきれいな数値ですが数値は当然ばらばらです。(もちろん、現代の工場で製作をする上では数値がきれいなことは重要ですが。)
根拠のある、合理的な共通の尺度から導き出される数値で、それが15の値でまとめられるということに感心しました。
6章 単なる道具
略
7章 実証と終節
要約
著者であるル・コルビュジエ氏自身が設計したもの”以外”の建築物や画についてモデュロールの数値や幾何学図形をあてはめて適合することを紹介しています。
感想
数値という1次元な尺度ならまだしも、幾何学的図形という2次元な尺度が画にも当てはまることに驚きました。
また同時に、解説を読んでも、どの図形をあてはめるのかは非常に難解だと感じました。
全体の感想
今まで本職の設計ではなんとなくのきりの良い寸法をとっていました。
モデュロールとは言わないまでも、日本人向けの設計なら、寸尺といった値をもとに根拠のある数値の合理化をすることもできるのではないかと感じました。(コストダウンにつながる様な寸法決定)
著者であるル・コルビュジエ氏が設計した、国立西洋美術館は当然モデュロールの比率で作られているので、展示物だけでなく建物そのものを見に行きたいと思いました。
以上
わかりやすいサイト:イラスト名建築ぶらり旅 with 宮沢洋&ヘリテージビジネスラボ⑬
筆者について
筆者 のびた
3DPなどを使って創作活動をしています。
BASEで販売をしています。
ツイッターはこちら




コメント